最近思考了一下，这个问题其实至少有 $\Theta((n\log n)^{1.5})$ 的算法，但实际效率目前只有理论意义。被 $\Theta(n^2)$ 暴力吊打，所以也出不了什么题，就直接把这个 idea 拿出来了。
定义平移指数基是这样一组基：$x^k \mathrm e^{r_k x}$，也就是说平移指数基变换是给一个数组 $a_k$ 和 $r_k$，求
$$ \sum_k a_k x^k \mathrm e^{r_k x} $$
我们考虑怎么算 $\sum _{0\le k < B} a_k x^k \mathrm e^{r_k x}$，注意如果我们能算这个，就可以转化成 $n/B$ 个问题，然后就是乘以 $x^B$，平移到对应的位置。
我们现在考虑一个 EGF 转 OGF，那其实就是 $\sum_k a_k \sum_n \frac{n! r_k^{n-k} x^n}{(n-k)!}$，而 $\sum_n \frac{n! r_k^{n-k} x^n}{(n-k)!} = k!\sum_n \binom n k r_k^{n-k}x^n = \frac{k!x^k}{(1-r_kx)^{k+1}}$。因此我们可以直接分治 FFT 计算 $\sum_k \frac{a_k k!x^k}{(1-r_kx)^{k+1}}$，最后分母的次数是 $\Theta(B^2)$ 的，复杂度是 $\Theta(B^2\log^2 B + n\log n)$（最后要再求逆一次）
因此复杂度是 $\Theta(nB\log^2 B + \frac{n^2}B\log n)$。在 $B=\Theta \left(\sqrt \frac{n}{\log n}\right)$ 的时候取到最优。复杂度为 $\Theta((n\log n)^{1.5})$。
事实上这个问题已经发现在一些地方会出现了……
例 1. 小 I 加好友（省内集训）
一个无向图，任意两点之间有 $p$ 的概率连边，接下来重复一个过程：如果有一个节点和 $1$ 号点的公共邻接点有至少 $K$ 个，就把它和 $1$ 连边。问无法操作后 $1$ 号点与所有点都连了边的概率是多少。$n\le 10^4$
经过容斥转化之后，我们容易发现答案 $f_n$ 转移满足一个形如这样的式子
$$ f_n = 1 - \sum_k \binom {n-1}{k-1} f_k r_k^{n-k} $$
其中 $r_k = [x^{K-1}]\frac{(q+px)^k}{1-x}$，并不是问题的瓶颈。
而这个递推式满足平移指数基变换的形式，它是半在线的，但是我们发现大小为 $B$ 的块内暴力转移并不影响复杂度。可以做到 $\Theta((n\log n)^{1.5})$。
例 2. 列欧拉数
求 $\langle {n\atop k} \rangle$，对于 $k\le n\le m$ 的所有 $n$。
我们先快进到 BGF $[t^n]\frac{(1-t)\mathrm e^{(1-t)x}}{1-t\mathrm e^{(1-t)x}}$。
为了简洁，这里推导 $[t^n]\frac1{1-t\mathrm e^{(1-t)x}}$，加上剩下的一些零碎部分是差不多的。
$$
\begin{aligned}&\quad[t^n]\frac1{1-t\mathrm e^{(1-t)x}}\\
&=x^n[t^n]\frac1{1-\frac tx\mathrm e^{(1-\frac tx)x}}\\
&=x^n[t^n]\frac1{1-\frac tx\mathrm e^{x-t}}\\
&=x^n[t^n]\frac1{1-t\mathrm e^{-t}(x\mathrm e^{-x})^{-1}}\\
&=\sum_k [t^n] (t\mathrm e^{-t})^{n-k} x^k\mathrm e^{(n-k)x}\\
&= \mathrm e^{nx}\sum_k [t^n] (t\mathrm e^{-t})^{n-k} (x\mathrm e^{-x})^k\\
&= \mathrm e^{nx}\sum_{0\le k\le n} \frac{(k - n)^k}{k!} (x\mathrm e^{-x})^k\end{aligned}
$$
最终结果算出来应该是
$$ \sum_{0\le k\le n} \frac{(-k-1)^{n-k}}{(n-k)!} x^{n-k}\mathrm e^{(k+1)x} - \sum_{1\le k\le n} \frac{(-k)^{n-k}}{(n-k)!} x^{n-k} \mathrm e^{kx} $$
这其实不仅符合我们之前那个基变换的形式，同时还是多项式复合 $F(x\mathrm e^{-x})$ 的形式。理论上有通过复合的 $\Theta((n\log n)^{1.5})$ 甚至 $n^{1+o(1)}$ 的算法。大概都不实用
例 3. 约束数列
给不降数列 $b$，$b_n = n$，问有多少正整数数列 $a_n$ 满足 $a$ 中有 $k$ 个数 $\le b_k$。
首先我们需要先确认一下不严格平移指数基变换的复杂度是相似的。这是说有长为 $n$ 的数列 $a_k, b_k, r_k$，要求
$$ \sum_k a_k x^{b_k} \mathrm e^{r_k x} $$
事实上这应该依然是可以 $\Theta ((n\log n)^{1.5})$ 的，我们按照 $b_k$ 所在的 $[(j-1)B, jB)$ 先看做一个格子，然后每个格子里如果累加到了 $\frac n{\log n}$ 就再切分。这样的话大约有 $\Theta(\frac nB + B\log n)$ 个组，合并部分的复杂度显然不超过 $\Theta(nB\log^2 n)$，若干次求逆不超过 $\Theta((\frac nB + B\log n)\log n)$，发现在 $B=\Theta \left(\sqrt {\frac n{\log n}}\right)$ 的时候仍是平衡的 $\Theta((n\log n)^{1.5})$。
对于原题来说，我们是在一个被 bound 住的路径下面做游走，同时一条路径的权值是对于每个高度 $h$，它所在这个高度下走的步长 $l_h$，那么路径的权值是 $\prod_h \frac1{l_h!}$。在如果横着走 $t$ 格，竖着走 $h$ 格的话，任意游走的权值和其实就是 $[x^t]\mathrm e^{hx}$。
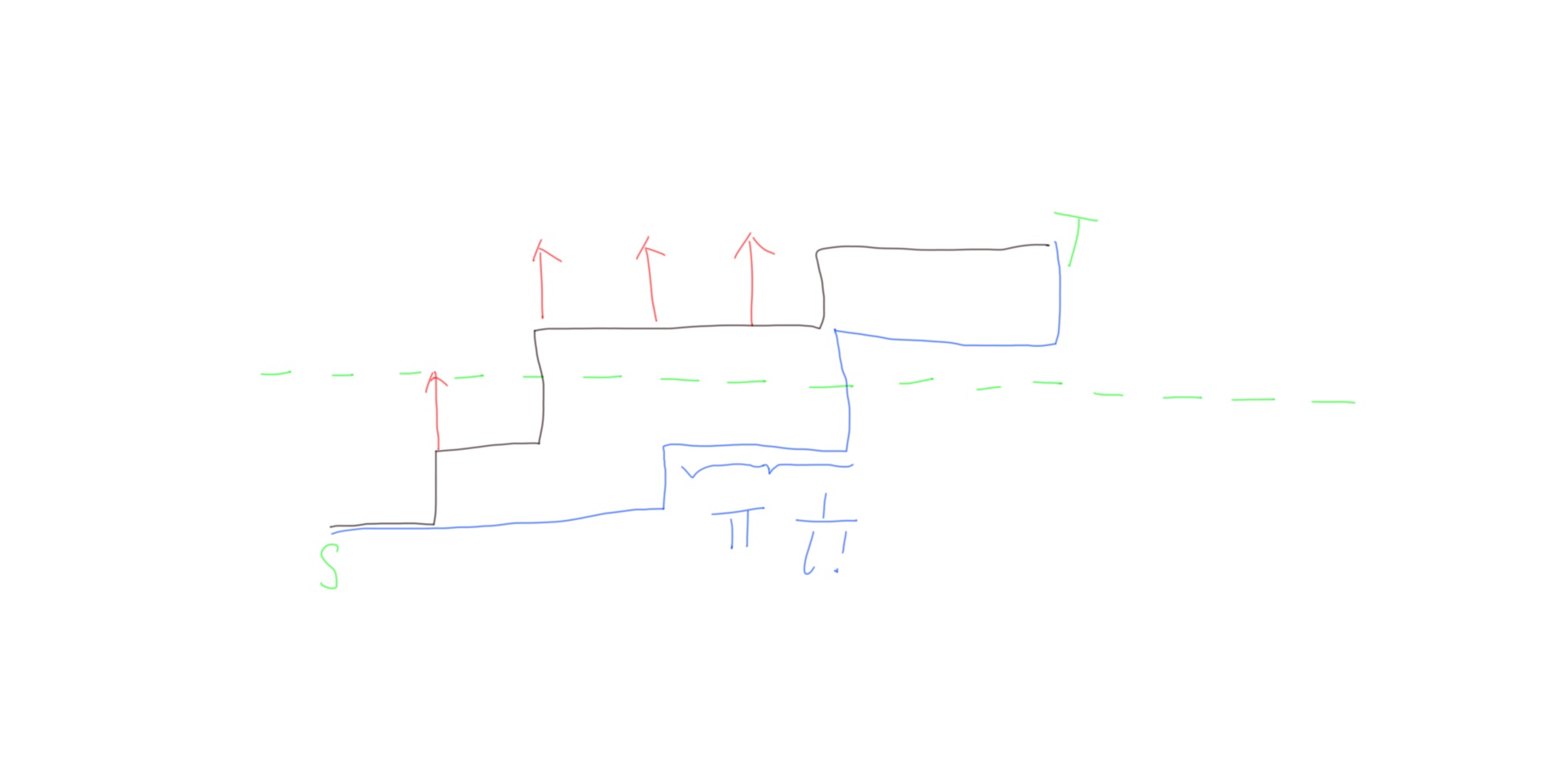注意到一个在 $(h,t)$ 位置的点往后对高度 $H$ 的贡献就是 $\mathrm e^{Hx} (x^t \mathrm e^{-hx})$，那么我们只需要进行不严格平移指数基变换。对于这个问题，我们不需要在外层分治了，因为里层的算法已经不是 $\tilde O(n)$ 的。值得注意的是现在还需要考虑一下块内的转移代价，暴力做已经是 $\Theta((sz)^2 \log n)$ 的（预处理所有幂听起来并不高效，而且这里多个 log 将会显示它不太影响复杂度），我们给每个 $sz > C$ 的块再切开，那么就是块数增加 $O(n/C)$ 个，复杂度多贡献了 $\Theta(nC\log n + \frac{n^2}C\log n)$。取 $C = \Theta(\sqrt n)$ 足够。不是复杂度瓶颈。
因此本问题也可以 $\Theta((n\log n)^{1.5})$ 解决。肯定跑得贼慢